離心近点角

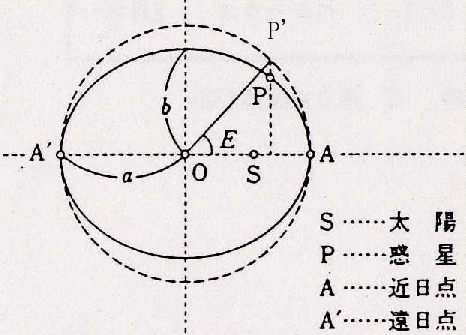
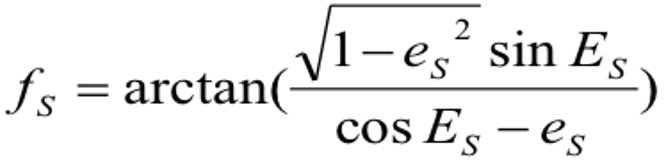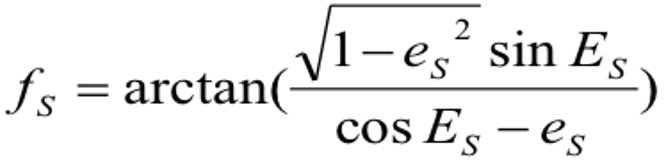離心近点角（りしんきんてんかく、英語: eccentric anomaly）とは、楕円軌道上の位置を表現する角度パラメータの一つである。楕円上の点を外接円上に長軸に対する垂線を共有するように射影するとき、近点に対して射影点がなす楕円の中心のまわりの角度である。

概要

長半径 a、短半径 b の楕円の方程式は

${\displaystyle {\frac {x^{2}}{a^{2}}} {\frac {y^{2}}{b^{2}}}=1}$

で与えられる。これを媒介変数を用いて

${\displaystyle x=a\cos E,~y=b\sin E}$

と表示したときの E が離心近点角である。

離心近点角は、楕円軌道を特徴付けるパラメータである離心率 e と長半径 a を用いて、軌道上の位置を指定するパラメータである中心天体（焦点）からの距離 r と

${\displaystyle r=a(1-e\cos E)}$

で関係付けることができる。また、真近点角 ν とは

${\displaystyle \cos \nu ={\frac {\cos E-e}{1-e\cos E}}}$

${\displaystyle \tan {\frac {\nu }{2}}={\sqrt {\frac {1 e}{1-e}}}\tan {\frac {E}{2}}}$

で関係付けることができる。

ケプラーの方程式

平均近点角 M は離心近点角と

${\displaystyle M=E-e\sin E}$

で関係付けられる。この関係式はケプラーの方程式と呼ばれる。

${\displaystyle e}$ (${\displaystyle e<0.6627434}$)の値は小さいため、${\displaystyle E_{0}=M}$ という初項を使って、漸化式 ${\displaystyle E_{i 1}=M e\sin E_{i}}$ によりこの方程式を解くことができる。最初の数項における e の冪級数は次のようになる。

${\displaystyle E=M e\sin M {\frac {e^{2}}{2}}\sin 2M {\frac {e^{3}}{8}}(3\sin 3M-\sin M) \dots }$

関連項目

• ケプラーの法則 - 楕円軌道
• 軌道要素 - 平均近点角 - 真近点角 - 射影近点角